Este es un curso de matemáticas de grado noveno, se encuentra en construcción, sirve como apoyo a los cursos de grado noveno del año 2022, 901, 902 y 903, acorde a los contenidos propuestos en nuestra malla curricular.
GUIA NÚMERO 6
ECUACIÓN DE LA RECTA DADO UN PUNTO Y LA PENDIENTE
1. Encuentra la ecuación de la recta y traza su grafica en cada uno de los siguientes casos:
GUIA NÚMERO 5
CONCEPTO DE PENDIENTE Y ECUACIÓN DE LA RECTA
TEOREMA DE PITAGORAS
Esta guía permite a los estudiantes de los cursos 901 y 902 con conectividad frente a la propuesta “aprende en casa “ tener una herramienta de trabajo virtual para abordar y comprender el tema de “Teorema de Pitágoras” siguiendo las temáticas propuestas en la malla curricular de matemáticas.
En la parte de contenido teórico se hace la presentación del tema y se da una explicación a base de ejemplos y en la parte de actividades se sugieren algunos videos, se proponen algunos ejercicios y se hace una pequeña evaluación virtual.
Esta es una guía explicativa, por tal motivo intenta manejar un lenguaje simple y ser muy minuciosa en las explicaciones.
En esta semana daremos inicio al tema "Teorema de Pitágoras" consignado en el plan de estudios.
EXPLICACION
El teorema de Pitágoras es un formula que permite hallar la medida de la longitud de uno de los lados de un triángulo rectángulo, conociendo la longitud de las medidas de los otros dos lados.
Para empezar el estudio es importante tener en cuenta que un triángulo rectángulo es aquel que tiene un ángulo recto, que el lado opuesto a ese ángulo es llamado hipotenusa y los otros lados catetos.
Ejemplo 1
Ejemplo 2:
Paso 4: Realizar la operación al interior de la raíz
2. Resuelva el siguiente problema:
Un estudiante observa un edificio de 195 metros de altura. Si la distancia de la terraza del edificio al estudiante es de 197 metros, ¿A cuántos metros está el estudiante de la entrada al edificio?
GUIA NUMERO 3
DISTANCIA ENTRE PUNTOS
Buenas tardes queridos estudiantes, espero se encuentren bien cuidando de si mismos y de las personas que están a su lado, en concordancia con el plan de estudios y con el tema visto anteriormente, para este periodo de tiempo comprendido entre el 18 de marzo y el 8 de abril, nos corresponde abordar el tema de distancia entre puntos.
La idea es hacer una explicación detallada del tema, proponer unos ejercicios para calificar y proponer también algunos videos tutoriales que les sirvan a ustedes como refuerzo.
Comencemos:
DISTANCIA
ENTRE PUNTOS
Por
haberlo estudiado, sabemos que el Plano Cartesiano se usa como un sistema de
referencia para localizar puntos en un plano.
Otra de
las utilidades de dominar los conceptos sobre el Plano cartesiano radica
en que, a partir de la ubicación de las coordenadas de dos puntos es posible
calcular la distancia entre ellos.
Ejemplo 1:
Hallar la distancia entre los puntos (–4, 0) y (5, 0)
Desarrollando las operaciones al interior de la raíz cuadrada tenemos:
Ejemplo 2:
Calcula la distancia entre los puntos P1(7, 5) y P2(4,
1)
Solución:
1. Identifiquemos en los puntos X1, X2, Y1 y Y2 así:
2. Reemplacemos en la fórmula:
3. Resolvamos las
operaciones que están al interior de la raíz cuadrada.
Actividad:
Resuelve el siguiente taller, lo puedes enviar resuelto, escaneado o fotografiado al correo caprietoo@educacionbogota.edu.co antes del 8 de abril, tendré en cuenta que su desarrollo esté claro, entendible y organizado. No olvides nuestras clases sincrónicas.
Hallar la distancia entre los siguientes puntos:
H(5, -3) y T( -1, 0)
2. L(-1, -4) y K(-2, -6)
3. O(0, 0) y M( -6, -7)
4. Q(-3, -6) y ( -6, -9)
5. J(-1/2, ¾) y W (3, 0)
VIDEO TUTORIAL
INTRODUCCIÓN A LA GEOMETRIA ANALITICA
Buenos días estimados estudiantes, ojalá se encuentren bien, les cuento que muy pocos estudiantes hicieron entrega de la primera guía que era como un abrebocas al curso de algebra que corresponde a este grado noveno, espero se pongan al día con esta sencilla tarea, para los que si entregaron le cuento que ya están publicadas sus notas por este mismo blog.
En esta semana daremos inicio al plan de estudios consignado en nuestra malla curricular cuyo primer tema de estudio es el plano cartesiano y cómo calcular la distancia entre dos puntos cualesquiera que estén en el plano cartesiano.
La idea es hacer lectura de la siguiente explicación, mirar los videos de apoyo, y resolver algunos ejercicios propuestos.
Comencemos:
PLANO CARTESIANO
Se conoce como plano cartesiano, coordenadas cartesianas o sistema cartesiano, a dos rectas numéricas perpendiculares, una horizontal y otra vertical, que se cortan en un punto llamado origen o punto cero.
La finalidad del plano cartesiano es describir la posición o ubicación de un punto en el plano, la cual está representada por el sistema de coordenadas.
El plano cartesiano también sirve para analizar matemáticamente figuras geométricas como la parábola, la hipérbole, la línea, la circunferencia y la elipse, las cuales forman parte de la geometría analítica.
El nombre del plano cartesiano se debe al filósofo y matemático francés René Descartes, quien fue el creador de la geometría analítica y el primero en utilizar este sistema de coordenadas.
Partes del plano cartesiano
Los elementos y características que conforman el plano cartesiano son los ejes coordenados, el origen, los cuadrantes y las coordenadas. A continuación, te explicamos cada uno.
Ejes coordenados
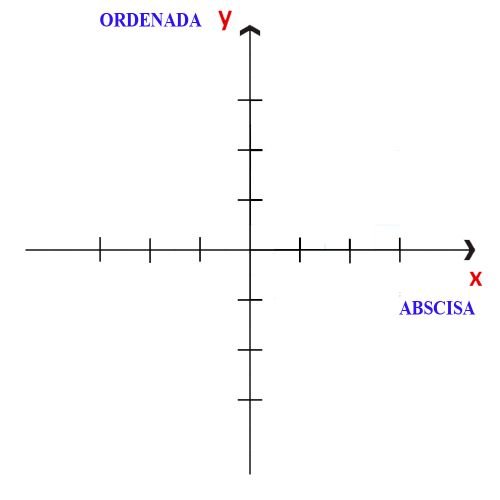
Se llaman ejes coordenados a las dos rectas perpendiculares que se interconectan en un punto del plano. Estas rectas reciben el nombre de abscisa y ordenada.
- Abscisa: el eje de las abscisas está dispuesto de manera horizontal y se identifica con la letra “x”.
- Ordenada: el eje de las ordenadas está orientado verticalmente y se representa con la letra “y”.
Origen o punto 0
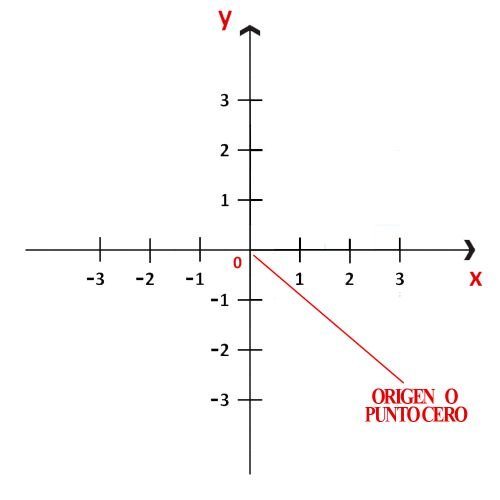
Se llama origen al punto en el que se intersecan los ejes “x” y “y”, punto al cual se le asigna el valor de cero (0). Por ese motivo, también se conoce como punto cero (punto 0). Cada eje representa una escala numérica que será positiva o negativa de acuerdo a su dirección respecto del origen.
Así, respecto del origen o punto 0, el segmento derecho del eje “x” es positivo, mientras que el izquierdo es negativo. Consecuentemente, el segmento ascendente del eje “y” es positivo, mientras que el segmento descendente es negativo.
Cuadrantes del plano cartesiano
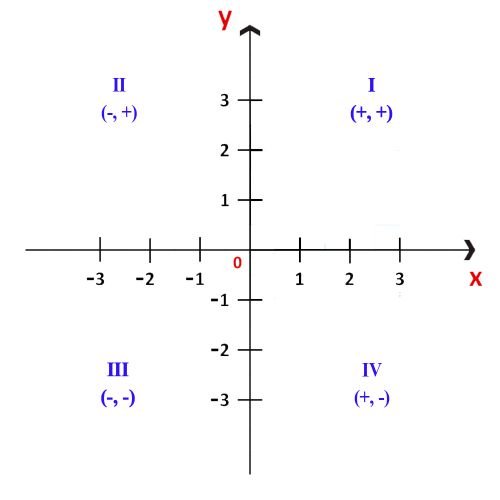
Se llama cuadrantes a las cuatro áreas que se forman por la unión de las dos rectas perpendiculares. Los puntos del plano se describen dentro de estos cuadrantes.
Los cuadrantes se enumeran tradicionalmente con números romanos: I, II, III y IV.
- Cuadrante I: la abscisa y la ordenada son positivas.
- Cuadrante II: la abscisa es negativa y la ordenada positiva.
- Cuadrante III: tanto la abscisa como la ordenada son negativas.
- Cuadrante IV: la abscisa es positiva y el ordenada negativa.
Coordenadas del plano cartesiano
Las coordenadas son los números que nos dan la ubicación del punto en el plano. Las coordenadas se forman asignando un determinado valor al eje “x” y otro valor al eje “y”. Esto se representa de la siguiente manera:
P (x, y), donde:
- P = punto en el plano;
- x = eje de la abscisa (horizontal);
- y = eje de la ordenada (vertical).
Si queremos saber las coordenadas de un punto en el plano, trazamos una línea perpendicular desde el punto P hasta el eje “x” –a esta línea la llamaremos proyección (ortogonal) del punto P sobre el eje “x”.
Seguidamente, trazamos otra línea desde el punto P hasta el eje “y” –es decir, una proyección del punto P sobre el eje “y”.
En cada uno de los cruces de las proyecciones con ambos ejes, se refleja un número (positivo o negativo). Esos números son las coordenadas.
Por ejemplo,
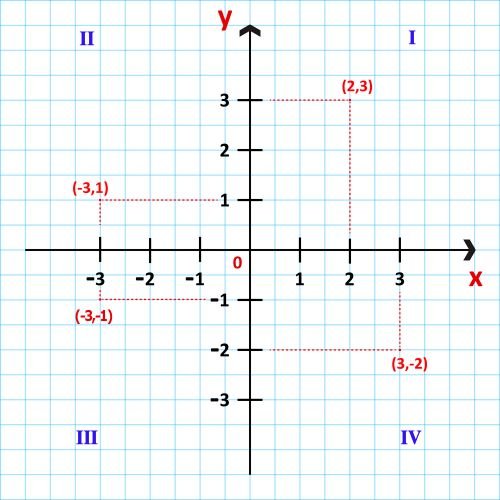
En este ejemplo, las coordenadas de los puntos en cada cuadrante son:
- cuadrante I, P (2, 3);
- cuadrante II, P (-3, 1);
- cuadrante III, P (-3, -1) y
- cuadrante IV, P (3, -2).
Si lo que queremos es saber la ubicación de un punto a partir de unas coordenadas previamente asignadas, entonces trazamos una línea perpendicular desde el número indicado de la abscisa, y otra desde el número de la ordenada. La intersección o cruce de ambas proyecciones nos da la ubicación espacial del punto.
Por ejemplo,
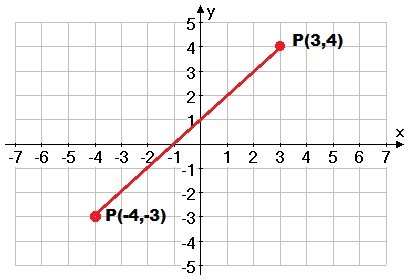
En este ejemplo, P (3,4) nos da la ubicación precisa del punto en el cuadrante I del plano. El 3 pertenece al eje de las abscisas y el 4 (segmento derecho) al eje de las ordenadas (segmento ascendente).
P (-3,-4) nos da la ubicación específica del punto en el cuadrante III del plano. El -3 pertenece al eje de las abscisas (segmento izquierdo) y el -4 al eje de las ordenadas (segmento descendente).
Video de apoyo:
Actividad:
Resuelve el siguiente taller, lo puedes enviar resuelto, escaneado o fotografiado al correo caprietoo@educacionbogota.edu.co antes del 10 de marzo, tendré en cuenta que su desarrollo ente claro, entendible y organizado. No olvides nuestras clases sincrónicas.
Hasta pronto.
GUÍA NUMERO 1
BIENVENIDA
Muy buen día estimados estudiantes, espero se encuentren bien, se que para muchos las cosas no han ido de la mejor manera desde que esta pandemia empezó, ha dejado estragos a nivel emocional y económico, pero de alguna manera hoy nos reunimos nuevamente con muchas ganas de salir adelante y comenzar este grado noveno. A la mayoría de ustedes ya los conozco y se de las capacidades de cada uno me siento muy feliz de poderlos tener nuevamente cómo mis estudiantes. Quiero que sepan que en este tiempo de pandemia los he extrañado mucho, y reflexionando encuentro que prima la vida y los buenos momentos. Quiero alentarlos para que sigan luchando y persiguiendo sus sueños, les soplo que hay mucha felicidad en el aprender, el aprender de la ciencia, los libros, los valles, las montañas, los mares, la humanidad, la historia. Sean buenas personas y no abandonen nunca el amor y la verdad por más caótico que vean el mundo. Les abrazo y aquí esta Camilo para ayudar.
En la universidad conocí a un amigo Willian Benavides que interpretaba un tema del maestro Argentino Fito Paez de forma magistral, a continuación encontrarán en un video esa canción, quiero dedicarles a todos ustedes esa canción cuyo mensaje es de aliento, "Yo vengo a ofrecer mi corazón":
Ahora mis niños debemos entrar en materia, les cuento que este año tendremos clases sincrónicas por la plataforma Teams, el primer encuentro se hará el día 22 de Febrero, y de ahí en adelante cada 20 días, la fecha puntual del próximo encuentro la fijaremos en cada clase. Por ahora tener muy presente que la primera clase sincrónica se realizará el día 22 febrero a la 1:45 pm por la plataforma Teams la invitación (Link ) será enviado a su correo institucional en los próximos dias. En este primer encuentro ofreceré una explicación de cómo será el trabajo con guías virtuales para éste 2021.
Actividad:
EL ALGEBRA
Como primera actividad les dejo un videíto acerca de la historia del Calculo, muy bonito. Véanlo, está relacionado con el énfasis del colegio, hagan una síntesis y la envían entes del 22 de febrero a mi correo escaneada o fotografiada. Mi correo es caprietoo@educacionbogota.edu.co ojo no es el mismo del año pasado.
El video es este:












































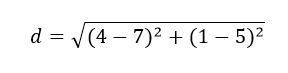





Profe ya le envie el trabajo numero 1
ResponderBorrarBuenas tardes profe, soy jhoan Gauta de 902, para informarle que no me a calificado la guía 5, que la envié por whatsapp el 31 de
ResponderBorrarmayo.